北京师范大学20 13 级普通师范生教学实习教案
(注:须于上课前二日写好)
部院系 数学科学学院 专业 数学与应用数学 实习生姓名 裴少君 学号 201311131111
部院系指导教师 李建华 实习学校教学指导教师 范先荣
2016 年 11 月 7 日 (星期 一 ) 第 一 节课 实习成绩 100
(本人本次实习第 3 个教案)
|
实习学校
|
北京科技大学附属中学
|
实习班级
|
高二六班
|
实习学科
|
数学
|
||
|
教学课题
|
空间直角坐标系
|
||||||
|
所用教材
|
教材名称: 数学B版 第 必修2 册,第 2 章 4 节 106 页
出版社: 人民教育出版社
|
||||||
|
教学目标
|
1. 学会如何建立空间直角坐标系,掌握点与坐标的对应关系
2. 探索空间直角坐标系八个卦限中的点以及各种特殊位置的点的坐标特点
3. 掌握空间两点的距离公式
4. 培养学生类比和化繁为简(降维)的数学思想,培养空间想象能力
|
||||||
|
教学重点
|
1. 在直线、平面和空间直角坐标系中,点与坐标之间的对应关系。
2. 空间两点的距离公式
|
||||||
|
教学难点
|
1. 确定点在空间直角坐标系中的坐标。
2. 空间两点距离公式的推导。
|
||||||
|
课时安排
|
1个课时
|
教学用具
|
三角板
|
||||
|
教学方法
|
引导式教学
|
||||||
|
教
学
过
程
及
内
容
|
(一) 新课引入
提问:数轴上几个实数能确定一点的位置?坐标平面上呢?
答:在数轴一个实数对应一个点;在平面上需要一对有序实数才能确定一点的位置。
提问:那么对于空间中的任一点呢?例如,我想要确定一架飞机在空中的位置,需要几个量来确定?
答:三个,经度,纬度,高度。
(二) 空间直角坐标系
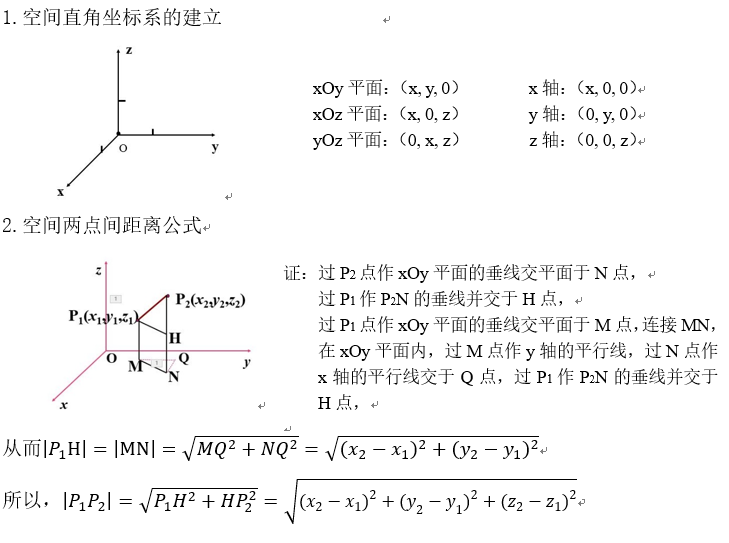
1. 空间直角坐标系的建立
为确定空间点的位置,我们在平面直角坐标系xOy的基础上,通过原点O,再做一条数轴z,是它垂直于xOy平面,由线面垂直的性质定理可得,z轴垂直于x轴,也垂直于y轴,这样它们中的任意两条都互相垂直。
轴的方向通常这样选择:从z轴的正方向看,x轴的正半轴沿逆时针方向旋转90°能与y轴的正半轴重合。这时,我们说在空间建立了一个空间直角坐标系Oxyz,O叫做坐标原点x轴,y轴,z轴叫做坐标轴,通过每两个坐标轴的平面叫做坐标平面,分别为xOy平面,yOz平面,xOz平面,坐标平面将空间分为8个卦限。
如何记这八个卦限呢?
以xOy为界,上方是一二三四卦限,下方是五六七八卦限,以x轴正方向看去,逆时针数,分别为一二三四,五六七八。
2. 坐标与点的一一对应关系
过P点分别做三个平面分别垂直于x,y,z轴,平面与三个坐标轴的交点分别为Px、Py、Pz,在其相应轴上的坐标依次为x,y,z,那么(x,y,z)就叫做点P的空间直角坐标,简称为坐标,记作P(x,y,z) 。
反之,任意给定三个实数的有序数组(x,y,z)就能够确定空间一个点的位置。
综上所述,空间中任意一点和三个实数的有序数组是一一对应的。
3. 特殊位置点的坐标特征以及对称点
坐标平面内的点:xOy平面(x,y,0); yOz平面(0,y,z);
xOz平面(x,0,z)。
问:空间中三个坐标分量的绝对值都为1的点有几个,写出来
目的:熟记八个卦限的位置,总结出每个卦限点的坐标的特点。
坐标轴上的点:x轴(x,0,0);y轴(0,y,0);z轴(0,0,z)
关于xOy平面的对称点(x,y,-z);关于xOy平面的对称点(x,-y,z)
关于yOz平面的对称点(-x,y, z)
关于x轴的对称点(x, -y, -z);关于y轴的对称点(-x, y, -z)关于z轴的对称点(-x, -y, z)。
总结:关于谁对称谁不变。
(三) 两点间的距离公式
首先回顾平面内两点间的距离公式,让学生类比猜想空间中的两点距离

目的:引导学生如何去设点,熟悉距离公式。
|
|
板
书
设
计
|
2.4空间直角坐标系
 |
|
课
后
总
结
与
评
议
记
录
|
自
我
分
析
和
同
学
评
议
意
见
|
设计很完整,前后承接很好,重点突出,知识深度的渗透很合适。
|
|
实
习
学
校
指
导
教
师
意
见
|
课堂设计完整,课堂容量很大,详略得当,学生积极性很高,课堂组织与把控很成功。
|
|
|
部
院
系
指
导
教
师
意
见
|
|
注:1.本表由实习生网上填写,每实习生四份。每一节新课(或连堂课)填写一份。
2.打印填写后由实习学校教学指导教师和我校的指导教师签字,部院系存档。
3.各部院系推荐的优秀教案打印后交教务处。