北京师范大学2013级普通师范生教学实习教案
（注：须于上课前二日写好）
部院系 数学科学学院 专业 数学与应用数学 实习生姓名 董晓宇 学号 201311131069
部院系指导教师 马波 实习学校教学指导教师 徐德前
2016 年 10 月 24 日 (星期 一 ) 第 二 节课 实习成绩
（本人本次实习第 2 个教案）
|
实习学校
|
北京宏志中学
|
实习班级
|
高一四班
|
实习学科
|
数学
|
||
|
教学课题
|
幂函数
|
||||||
|
所用教材
|
教材名称： 高中数学A版必修一 ，第 二 章 2.3 节 77-78 页
出版社： 人民教育出版社
|
||||||
|
教学目标
|
1．知识与技能：理解幂函数的概念，通过具体实例研究幂函数的图象和性质，并初步进行应用.
2．过程与方法：通过对幂函数的学习，使学生进一步熟练掌握研究函数的一般思想方法.
3．情感、态度与价值观：进一步渗透数形结合、分类讨论的思想方法；通过引导学生主动参与作图、分析图象，培养学生的探索精神.
|
||||||
|
教学重点
|
通过五个具体幂函数认识幂函数的一些性质
|
||||||
|
教学难点
|
画五个幂函数的图象并由图象概括其性质
|
||||||
|
课时安排
|
1课时
|
教学用具
|
几何画板
|
||||
|
教学方法
|
讲授法
问答法
引导发现法
教具演示法
|
||||||
|
教
学
过
程
及
内
容
|
一、复习旧知，创设情景
这就是我们这节课要学习的一种新的函数——幂函数. 二、探索新知，思考总结
首先，来看幂函数的定义：
一般地，函数
 叫做幂函数，其中x是自变量，a是常数. 可以看出，幂函数的自变量x是幂的底数，换句话说，幂的底数是单变量x，幂指数是个常数，幂的系数是1，符合上述形式的函数，就是幂函数.
我们可以发现，幂函数和指数函数的形式看起来有些像，都是幂的形式，它们的不同点就在于自变量的位置是不同的，幂函数是底数作为自变量，指数为常数，而指数函数则是指数作为自变量，而底数为常数，在以后的学习中要注意区分这两种函数.
【练习】
1、以下函数哪些是幂函数？
 2、已知幂函数 y="f(x) 图象过点（2，
 ）, 试求出这个函数的解析式.幂函数总体来说是一种比较复杂的函数，因此我们不对幂函数做整体性质的讨论，只讨论几个常见情况，分别是 a 取1，2，3，
  和 -1 的情况，也就是讨论这样五个函数 其中，
 这3个函数是我们熟悉的，分别是一次函数、二次函数和反比例函数，由此我们也知道，幂函数与我们以前学过的一些函数是有交叉的，并不是完全陌生的函数. 下面我们就来讨论一下这5个幂函数. 可以想一想，我们现在一般会从哪些方面对函数进行研究呢？我们需要了解函数的定义域、图象、以及它们的单调性、奇偶性等性质. 首先，在同一直角坐标系内作出这5个幂函数的图象. 要注意画函数图象的步骤为：列表，描点、连线.
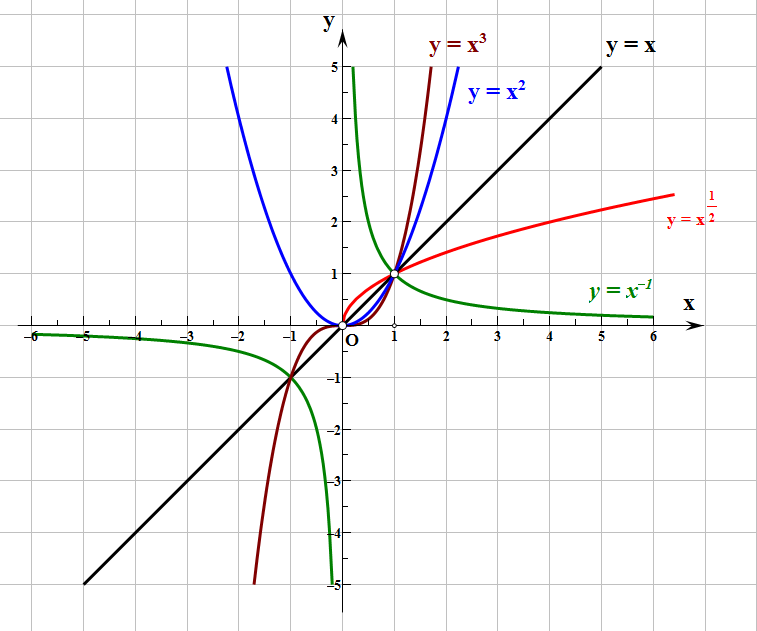
下面，结合所画图象，讨论这几个函数的性质，请同学们先仔细思考，完成学案上的表格.
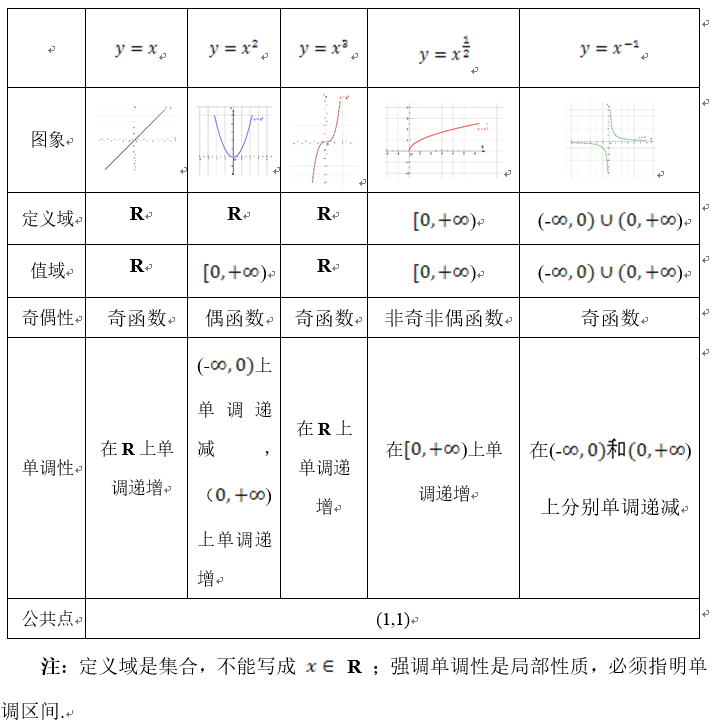
   三、课堂总结 本节课我们通过学习了幂函数的概念，结合图象，对几个常见的幂函数的定义域、图象、奇偶性、单调性有了一定的了解，其中，根据函数图象来猜想性质，这是运用了数形结合的思想方法，这在今后的的学习，尤其是函数和将来的解析结合学习中将是一种十分重要的思想方法.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
板
书
设
计
|
|
|
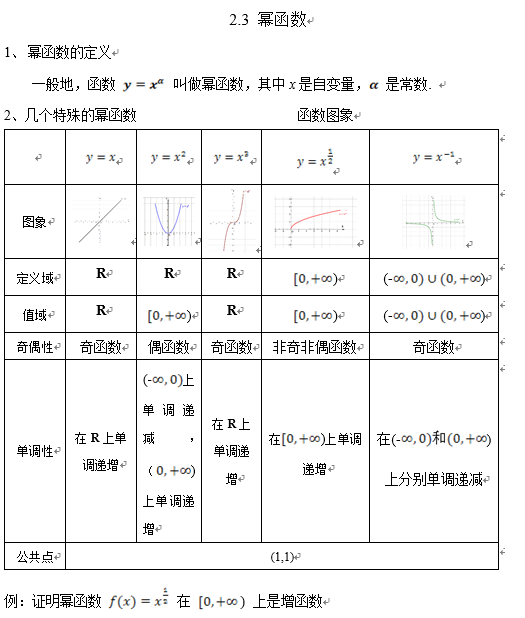
课
后
总
结
与
评
议
记
录
|
自
我
分
析
和
同
学
评
议
意
见
|
自我分析：
在本节中，学生的自主探究能力得到了充分的发挥，但也由于学生总体基础较差，探究过程中尽管有教师的引导，但进展仍比较缓慢，导致课堂节奏比预设及试讲要慢，从而压缩了练习的时间。总体而言，本节课总体效果较好，课堂任务也基本完成，相信学生的自主学习能力也可以有所提高。
同学评议：
董晓宇同学授课大方，表达流利，教态自然，能较熟练地运用现有教学设备，采用多种教学手段促使学生思考。
|
|
实
习
学
校
指
导
教
师
意
见
|
董晓宇同学仔细研读教材，认真备课，教学设计合理，在教学过程中，能够做到思维严谨、表述清晰，突出了知识的重点和难点，有效调动了学生学习的主动性，收到很好的教学效果。具备良好的教师职业素质。
|
|
|
部
院
系
指
导
教
师
意
见
|
同意实习学校指导教师意见。
|
注：1.本表由实习生网上填写，每实习生四份. 每一节新课（或连堂课）填写一份.
2.打印填写后由实习学校教学指导教师和我校的指导教师签字，部院系存档.
3.各部院系推荐的优秀教案打印后交教务处.